2024 MAA AMC 10A

题目1

\( {101} \cdot 9,{901} - {99} \cdot {10},{101} \) 的值是多少？

(A) 2 (B) 20 (C) 21 (D) 200 (E) 2020

题目2

将 2024 写成若干个两位数的和，这些两位数不一定互不相同。问最少需要多少个两位数？

(A) 20 (B) 21 (C) 22 (D) 23 (E) 24

题目3

用于估算沿山间小径登顶所需时间的模型形如 \( T = {aL} + {bG} \) ，其中 \( a \) 和 \( b \) 为常数， \( T \) 为时间(分钟)， \( L \) 为小径长度(英里)， \( G \) 为海拔提升(英尺)。模型估计，若小径长 1.5 英里且海拔提升 800 英尺，需 69 分钟登顶；若小径长 1.2 英里且海拔提升 1100 英尺，同样需 69 分钟登顶。若小径长 4.2 英里且海拔提升 4000 英尺，模型估计需多少分钟登顶？

(A) 240 (B) 246 (C) 252 (D) 258 (E) 264

题目4

设 \( n \) 为可表示为 5 个不同质数之和的最小质数，求 \( n \) 的各位数字之和。

(A) 5 (B) 7 (C) 8 (D) 10 (E) 11

题目5

使得 \( n! \) 是 2024 的倍数的最小正整数 \( n \) 是多少？

(A) 11 (B) 21 (C) 22 (D) 23 (E) 253

题目6

将字符串 ABCDEF 变为 FEDCBA 所需的最少相邻字母交换次数是多少？(例如，将 ABC 变为 CBA 需要 3 次交换；一个这样的交换序列是 \( \mathrm{{ABC}} \rightarrow \mathrm{{BAC}} \rightarrow \mathrm{{BCA}} \rightarrow \mathrm{{CBA}} \) 。)

(A) 6 (B) 10 (C) 12 (D) 15 (E) 24

题目7

Amy、Bomani、Charlie 和 Daria 在一家巧克力工厂工作。周一，Amy、Bomani 和 Charlie 于下午 1:00 开始工作，每 3 分钟分别能封装 4、3、3 个包裹。稍后，Daria 加入，她每 4 分钟能封装 5 个包裹。他们一起在下午 2:45 准时完成了 450 个包裹的封装。Daria 是何时加入的？

(A) 1:25 PM (B) 1:35 PM (C) 1:45 PM (D) 1:55 PM (E) 2:05 PM

题目8

三个整数的乘积为 60。这三个整数的最小正和是多少？

(A) 2 (B) 3 (C) 5 (D) 6 (E) 13

题目9

6 名大三学生和 6 名大四学生可以组成 3 个互不重叠的 4 人小组，每个小组有 2 名大三学生和 2 名大四学生，共有多少种方式？

(A) 720 (B) 1350 (C) 2700 (D) 3280 (E) 8100

题目10

有多少个有序整数对 (m, n) 满足 \( \sqrt{{n}^{2} - {49}} = m \) ？

(A) 1 (B) 2 (C) 3 (D) 4 (E) 无穷多个

题目11

考虑以下操作:给定一个正整数 \( n \) ，若 \( n \) 是 3 的倍数，则将 \( n \) 替换为 \( \frac{n}{3} \) ；若 \( n \) 不是 3 的倍数，则将 \( n \) 替换为 \( n + {10} \) 。然后继续这一过程。例如，从 \( n = 4 \) 开始，该过程得到 \( 4 \rightarrow {14} \rightarrow {24} \rightarrow 8 \rightarrow {18} \rightarrow 6 \rightarrow 2 \rightarrow \) \( {12} \rightarrow \cdots \) 。假设从 \( n = {100} \) 开始，若恰好执行此操作 100 次，将得到什么值？

(A) 10 (B) 20 (C) 30 (D) 40 (E) 50

题目12

塞尔达于 8 月 1 日玩《数学冒险》游戏，得分为 1700 分。她在接下来的 5 天里每天继续游玩。下方的柱状图显示了她每天相对于前一天的得分变化。(例如，塞尔达 8 月 2 日的得分为 \( {1700} + {80} = {1780} \) 分。)问这 6 天内她的平均得分是多少分？

从 8 月 2 日至 6 日的每日得分变化

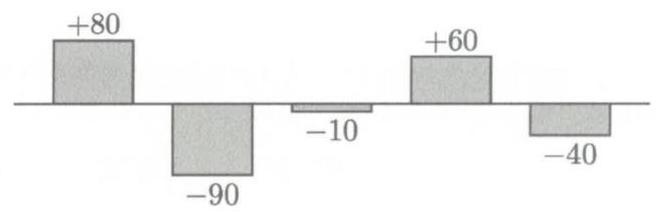
\( \begin{array}{lllll} \text{ Aug }2 & \text{ Aug }3 & \text{ Aug }4 & \text{ Aug }5 & \text{ Aug }6 \end{array} \)

(A) 1700 (B) 1702 (C) 1703 (D) 1713 (E) 1715

题目13

若先执行第一种变换再执行第二种变换，与先执行第二种再执行第一种得到的结果相同，则称这两种变换可交换。考虑坐标平面的以下四种变换:

• 向右平移 2 个单位，
• 绕原点逆时针旋转 \( {90}^{ \circ } \) ，
• 关于 \( x \) 轴的反射，以及
• 以原点为中心、比例因子为 2 的位似变换。

在这 6 组不同的变换对中，有多少组可交换？

(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

题目14

设 \( M \) 是使得 \( M + {1213} \) 和 \( M + {3773} \) 都是完全平方数的最大整数。问 \( M \) 的个位数字是几？

(A) 1 (B) 2 (C) 3 (D) 6 (E) 8

题目15

高为 24 的等边三角形的一条边位于直线 \( \ell \) 上。半径为 12 的圆与直线 \( \ell \) 相切，并且与三角形外切。在三角形和圆的外部，由三角形、圆、直线 \( \ell \) 所围成的区域的面积可以表示为 \( a\sqrt{b} - {c\pi } \) ，其中 \( a, b \) 是正整数，且 \( c \) 不能被任何质数的平方整除。问 \( b \) 是多少？

(A) 72 (B) 73 (C) 74 (D) 75 (E) 76

题目16

在按比例绘制的下图中，所有矩形都与整个的大矩形相似。每个数表示其所在矩形的面积。问 \( {AB} \) 的长度是多少？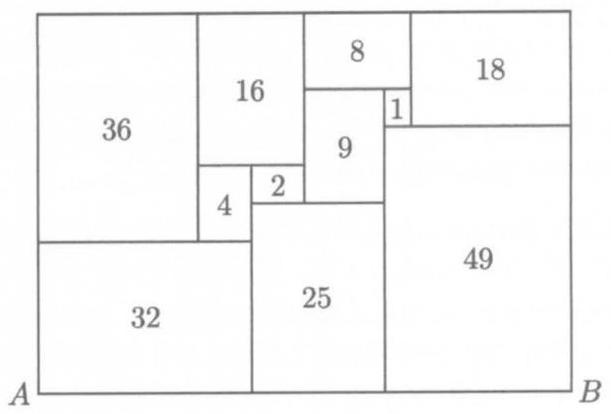



(A) \( 4 + 4\sqrt{5} \) (B) \( {10}\sqrt{2} \) (C) \( 5 + 5\sqrt{5} \) (D) \( {10}\sqrt[4]{8} \) (E) 20

题目17

恰好有 \( K \) 个正整数 \( b \) 满足 \( 5 \leq b \leq {2024} \) ，使得 \( b \) 进制整数 \( {2024}_{b} \) 能被 16(16 为十进制)整除。 \( K \) 的各位数字之和是多少？

(A) 16 (B) 17 (C) 18 (D) 20 (E) 21

题目18

一个等比数列的前三项是整数 \( a,{720} \) ，且 \( b \) ，其中 \( a < {720} < b \) 。问 \( b \) 的最小可能值的各位数字之和是多少？

(A) 9 (B) 12 (C) 16 (D) 18 (E) 21

题目19

两队进行三局两胜制季后赛:两队最多打 3 场，先赢 2 场者获胜。第一场在 A 队主场，其余在 B 队主场。A 队主场胜率 \( \frac{2}{3} \) ，客场胜率 \( p \) 。各场比赛结果独立。A 队夺冠概率为 \( \frac{1}{2} \) 。则 \( p \) 可写成 \( \frac{1}{2}\left( {m - \sqrt{n}}\right) \) 的形式，其中 \( m \) 与 \( n \) 为正整数。问 \( m + n \) 是多少？

(A) 10 (B) 11 (C) 12 (D) 13 (E) 14

题目20

设 \( S \) 是 \( \{ 1,2,3,\ldots ,{2024}\} \) 的子集，满足以下两个条件:
• 若 \( x \) 和 \( y \) 是 \( S \) 中的不同元素，则 \( \left| {x - y}\right| > 2 \) 。
• 若 \( x \) 和 \( y \) 是 \( S \) 中的不同奇元素，则 \( \left| {x - y}\right| > 6 \) 。

\( S \) 中元素的最大可能数量是多少？

(A) 436 (B) 506 (C) 608 (D) 654 (E) 675

题目21

一个 \( 5 \times 5 \) 整数数组的每一行按顺序构成一个长度为5的等差数列，每一列按顺序也构成一个长度为5的等差数列。已知位置 \( \left( {5,5}\right) ,\left( {2,4}\right) ,\left( {4,3}\right) \) 和(3,1)处的数分别为0,48,16和12。问位置(1,2)处的数是多少？

\[ \left\lbrack \begin{matrix} . & ? & . & . & . \\ . & . & . & {48} & . \\ {12} & . & . & . & . \\ . & . & {16} & . & . \\ . & . & . & . & 0 \end{matrix}\right\rbrack \]

(A) 19 (B) 24 (C) 29 (D) 34 (E) 39

题目22

整数 \( a, b \) 和 \( c \) 满足 \( {ab} + c = {100},{bc} + a = {87} \) 和 \( {ca} + b = {60} \) 。问 \( {ab} + {bc} + {ca} \) 是多少？

(A) 212 (B) 247 (C) 258 (D) 276 (E) 284

题目23

设 \( \mathcal{K} \) 是由两个直角三角形沿公共斜边拼接而成的筝形，这两个直角三角形的直角边分别为1和 \( \sqrt{3} \) 。用8个 \( \mathcal{K} \) 拼成下图所示的多边形。求三角形 \( \bigtriangleup {ABC} \) 的面积。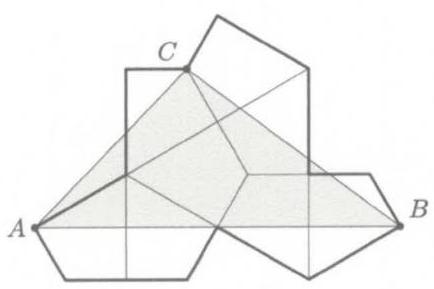

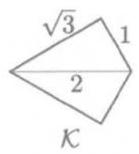
(A) \( 2 + 3\sqrt{3}\; \) (B) \( \frac{9}{2}\sqrt{3} \) (C) \( \frac{{10} + 8\sqrt{3}}{3} \) (D) 8 (E) \( 5\sqrt{3} \)

题目24

一只蜜蜂在三维空间中移动。一个公平的六面骰子，其六个面分别标有 \( {A}^{ + },{A}^{ - },{B}^{ + },{B}^{ - },{C}^{ + } \) 、 \( {C}^{ - } \) 。假设蜜蜂位于点(a, b, c)。如果骰子显示 \( {A}^{ + } \) ，蜜蜂就移动到点 \( \left( {a + 1, b, c}\right) \) ；如果骰子显示 \( {A}^{ - } \) ，蜜蜂就移动到点 \( (a - \) \( 1, b, c) \) 。其余四种结果也按类似方式移动。假设蜜蜂从点(0,0,0)出发，骰子掷四次。蜜蜂恰好经过某个单位立方体的四条不同边的概率是多少？

(A) \( \frac{1}{54} \) (B) \( \frac{7}{54} \) (C) \( \frac{1}{6} \) (D) \( \frac{5}{18} \) (E) \( \frac{2}{5} \)

题目25

下图所示为一个宽8格、高3格的虚线网格，共由 \( {1}^{\prime \prime } \times {1}^{\prime \prime } \) 个正方形组成。Carl沿某些正方形的边放置1英寸长的牙签，以构成一条不自相交的闭合回路。方格中的数字表示该正方形被牙签覆盖的边数；若方格内无数字，则其被覆盖的边数不受限制。Carl有多少种放置牙签的方法？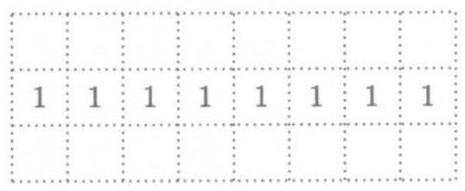

(A) 130 (B) 144 (C) 146 (D) 162 (E) 196